[143] Large-scale topology optimization for dynamic problems using a repetitive substructuring approach
H. S. Koh and G. H. Yoon. Structural and Multidisciplinary Optimization 67 (3), 33
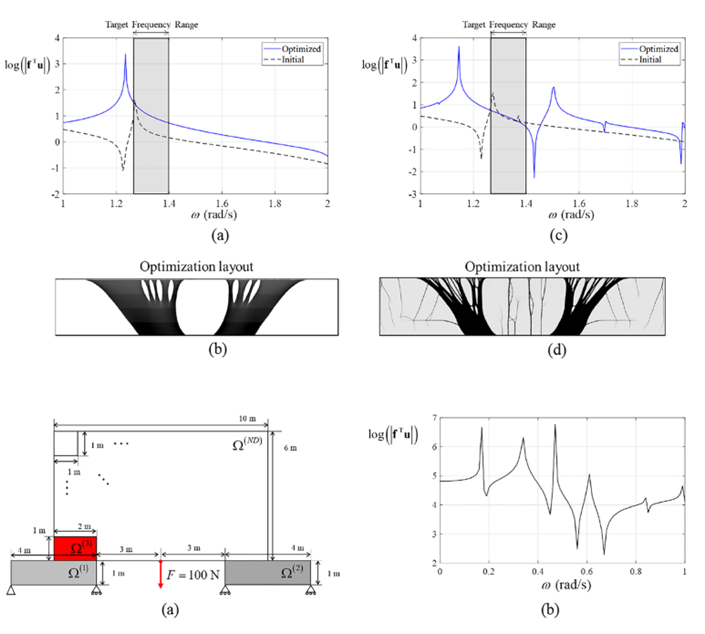
This paper proposes a novel technique for large-scale partial topology optimization of dynamic engineering structures by utilizing substructuring techniques and repetitive geometry. Partial topology optimization refers to a design domain that only covers a part of the overall analysis domain, involving multiple subdomains. While large-scale topology optimization techniques for static systems have made significant progress over the past few decades, techniques for dynamic systems, especially those in the frequency domain, face challenges due to matrix conditioning and preconditioning problems for iterative solvers. To overcome these challenges, this paper dramatically reduces the system's size through a substructuring approach to utilize a direct linear solver. Using a bottom-up style substructuring technique, all the finite element (FE) models are defined separately and in parallel, and the FE models in the non-design domains are approximated using the idea of repetitive geometry with the same discretization, while the models in the design remain intact. This approach eliminates conventional model reduction-based topology optimization problems, such as eigen-analysis and recovery processes for every iteration. The proposed technique enables a more realistic and feasible design of large-scale engineering structures in the frequency domain. Several numerical examples verify the performance of the presented method for partial topology optimization of large-scale models. Overall, this paper provides a novel and efficient approach to partial topology optimization for dynamic engineering structures, opening up new possibilities for realistic and feasible design in the frequency domain.
| 첨부파일 |
|---|