[122] Eigensensitivity of damped system with distinct and repeated eigenvalues by chain rule
T. Phuor and G. H. Yoon. International Journal for Numerical Methods in Engineering (2022).
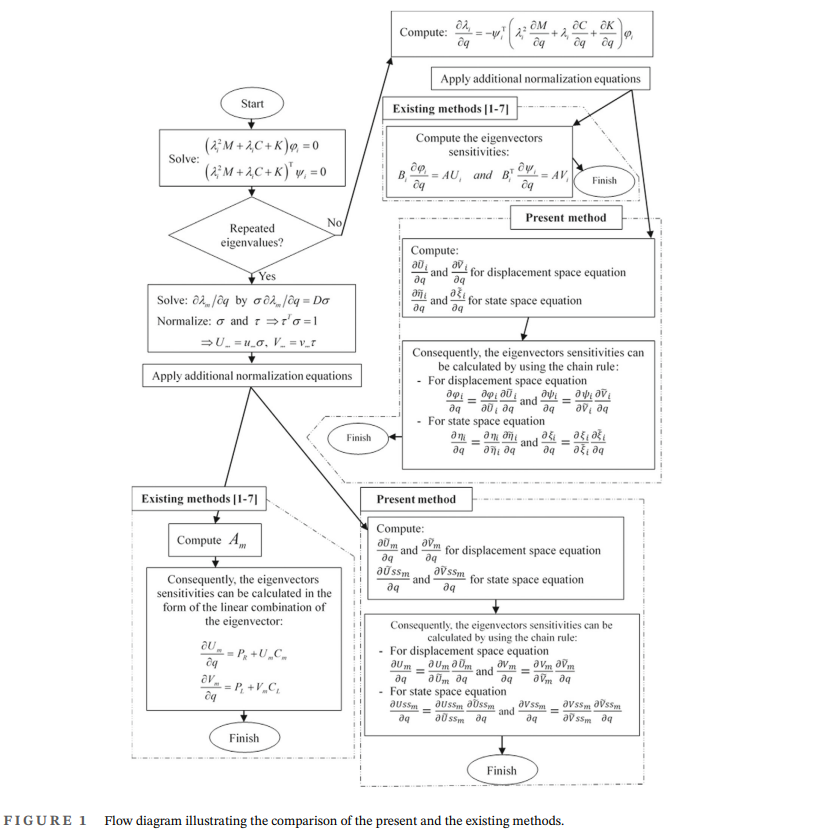
In this paper, a novel algorithm for computing the derivatives of eigensolutions of asymmetric damped systems with distinct and repeated eigenvalues is developed without using second-order derivatives of the eigenequations, which has a significant benefit over the existing published methods. To achieve this, the algorithm is proposed by (1) imposing consistent normalization conditions for both left and right eigenvectors throughout the computational system, and (2) solving sensitivity problems using the chain rule. These contributions add significant value to the proposed method. Additionally, the numerical difficulty is overcome by suggesting justifying Nelson (1976)'s technique based on the normalization conditions. Even though the proposed algorithm is simple and easy to implement, the employment of chain rule with new normalization in this note has never been reported in the literature, especially for the problem of eigensensitivity. Because this new algorithm does not require the second-order derivatives of the eigenequations, the analytical and numerical solutions for eigensensitivity offered by this method are less complicated than existing available solutions. The validity and applicability of the method are demonstrated through five numerical examples, showcasing its implementation in displacement- and state-space equations (rotordynamic system). Also, verifications are found to be in reasonable agreement with the approximated method.