[82] Stress constraint topology optimization using layerwise theory for composite laminates
J. W. Lee, J. J. Kim, and G. H. Yoon. Composite Structures 226 (2019): 111184.
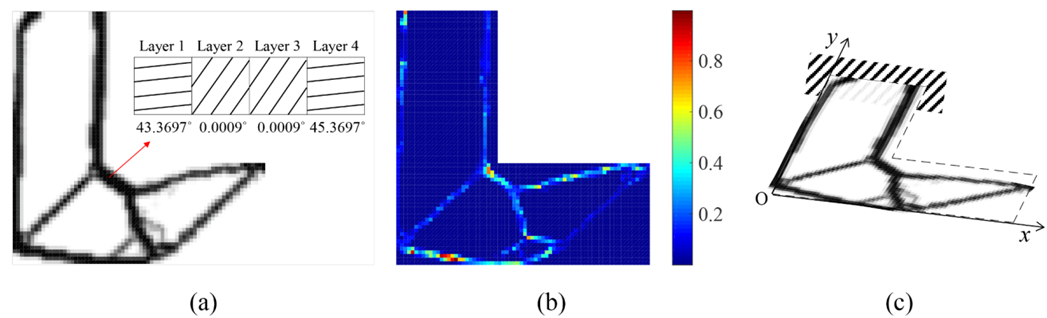
An improved stress-based topology optimization method for laminated composites is proposed by applying the layerwise theory in this research. The layerwise theory is an analysis technique for laminated composites or fiber-reinforced composites that has been developed to overcome the disadvantages of the classical laminated plate theory (CLPT). Because transverse shear deformation is ignored in the CLPT, it cannot be used for thick plates or multiple-layered composites. Therefore, new methods have been developed for analyzing them, and one of them is the layerwise theory. Using the layerwise theory, it is possible to accurately analyze a thick plate and predict the behavior of multiple layers of composites. In the layerwise theory, because a new displacement field and a modified finite element (FE) model are used, the FE model of the stress-based topology optimization method (STOM) is reconstructed to apply the layerwise theory. To apply the STOM for composite materials, the specific failure criterion developed for anisotropic materials must be selected. Therefore, the Tsai–Hill criterion and Tsai–Wu criterion are adapted to the STOM formula to consider the failure of composite materials. Further, the orientation of each layer in a composite significantly affects the optimization result as well as stiffness. Therefore, in this study, we optimize the density and orientation simultaneously by setting the orientation as a design variable. Finally, several types of p-norm approaches are proposed, and one of them can be chosen depending on the location of the maximum value of the constraint.