[80] Topology optimization of functionally-graded lattice structures with buckling constraints
작성자 관리자
날짜 2023-12-26 16:22:11
조회수 94
B. Yi, Y. Q. Zhou, G. H. Yoon, and K. Saitou. Computer Methods in Applied Mechanics and Engineering 354 (2019): 593-619.
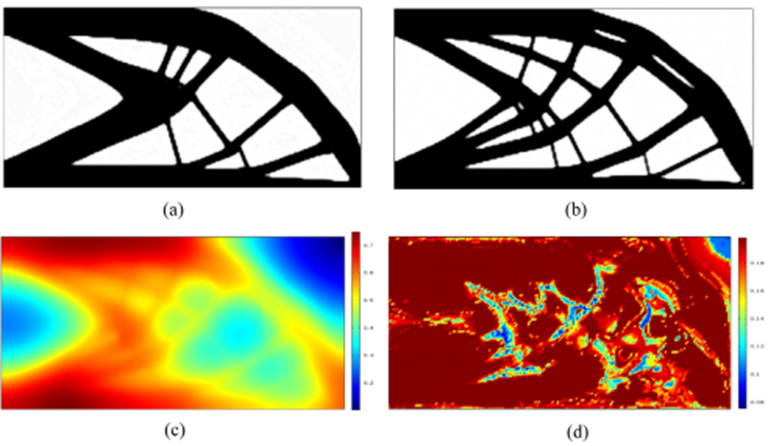
Lattice structures have been widely studied due to their advantage of low stiffness-to-weight ratio or sometimes auxetic properties. This paper presents a topology optimization method for structures with functionally-graded infill lattices with buckling constraints, which minimizes compliance while ensuring a prescribed level of structural stability against buckling failures. To realize topologically-optimized structures filled with functionally-graded lattices, Helmholtz PDE-filter with a variable radius is applied on the density field in Solid Isotropic Material with Penalization (SIMP) method. Buckling load factors based on the linear buckling analysis is employed as buckling constraints. Numerical examples show that proposed method can generate stiff structures comparable to the ones by the SIMP, with functionally-graded infill lattices that improve the structural stability by avoiding long, slender features under compression.