[29] Toward a multifrequency quasi‐static Ritz vector method for frequency‐dependent acoustic system application
G. H. Yoon. International journal for numerical methods in engineering 89, no. 11 (2012): 1451-1470.
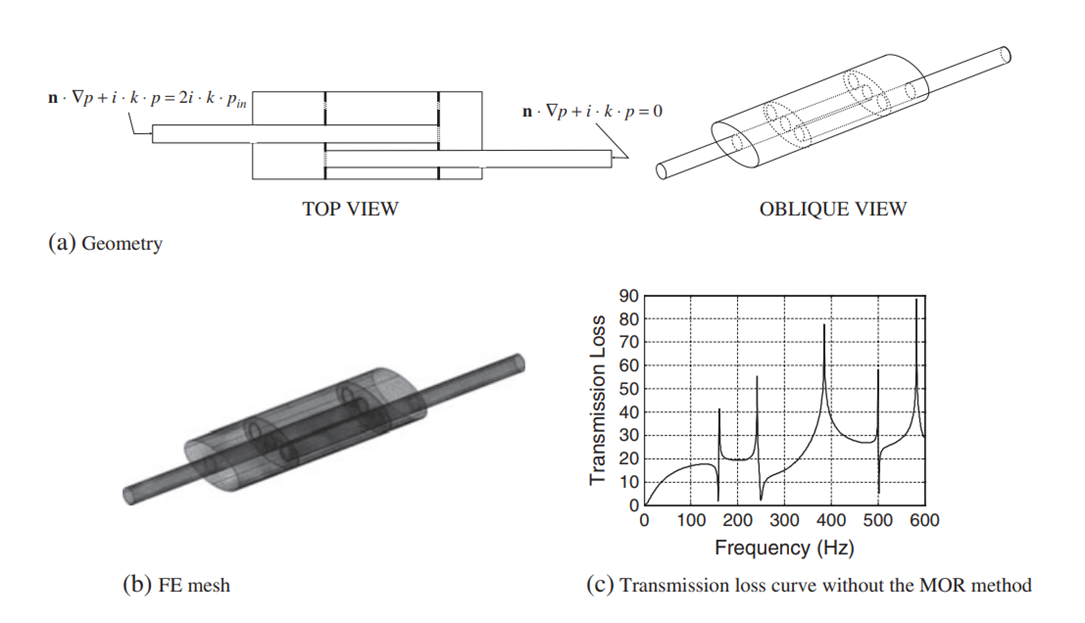
Computational issues concerning the calculation of acoustic responses of a complex finite element (FE) model for various noise and vibration inputs have become prevalent. Such a model requires a significant amount of computation time because of repeated inversions of dynamic stiffness matrices. Thus, even state of-the-art computer hardware and software often face limitations where a model order reduction (MOR) scheme can help. The established MOR schemes such as Ritz vector or quasi-static Ritz vector methods are efficient for general engineering systems, but these MOR methods become inaccurate for frequency response analyses in some acoustic systems with frequency-dependent mass and stiffness matrices and force vectors (hereinafter frequency-dependent acoustic systems). To cope with the inaccurate prediction by these methods for frequency-dependent acoustic systems, this research presents and applies the multifrequency quasi-static Ritz vector method. Unlike the Ritz vector or quasi-static Ritz vector methods, the present multifrequency quasi-static Ritz vector method employs direct Krylov subspace bases without an orthonormal procedure at multiple center frequencies. In comparison with the existing MOR scheme, a significant gain in computational efficiency is achieved, as well as enhanced accuracy. A comparison of these methods based on criteria such as efficiency, accuracy, and reliability was also conducted.