[138] Ritz vector-based substructuring method using interface eigenmode-shape pseudo-forces
작성자 관리자
날짜 2024-01-15 15:05:17
조회수 39
H. S. Koh and G. H. Yoon. Finite Elements in Analysis and Design 227 (2023): 104023.
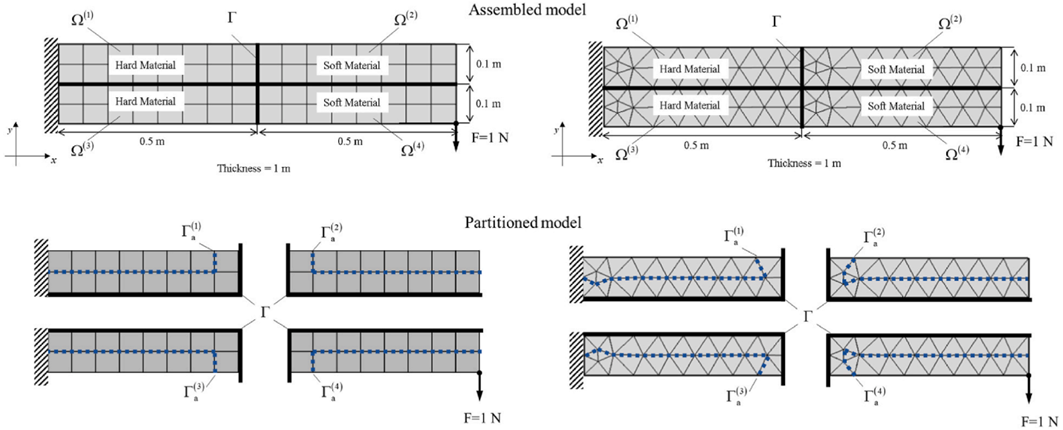
We propose a new Ritz vector-based dynamic substructuring method which substitutes the unit pseudo-forces applied at the adjacent degrees of freedom (DOFs) using distributed forces. One of the main problems of the Ritz vector and unit pseudo-force-based dynamic substructuring method is the strong dependence of the number of reduction bases on the interface DOF, which is not reduced by substructuring. This type of dependency causes the number of reduction bases obtained by the unit pseudo-forces to be always exceed or at least equal to the number of interface DOFs. The number of Ritz vector bases required at adjacent interface DOFs is efficiently reduced by approximating the unit pseudo-force as a type of distributed force using an energy transfer approach. The distributed forces, called eigenmode-shape pseudo-forces, comprise low modes computed through the eigenvalue problem of substructures corresponding to adjacent DOFs, and a set of distributed forces is a subspace of the vector space spanned by the unit force vectors. The efficiency of the substructuring method may be increased by reducing the number of reduction bases. This approach was demonstrated through several numerical examples.